프로세서의 발전 및 구조
컴퓨터 프로세서는 2000년대 초반까지 매우 빠르게 발전해왔다.
- 인텔 8086(1981): 5MHz
- 인텔 80486(1989): 25MHz
- 펜티엄 (1993): 66MHz
- 펜티엄 4(2000): 1.5 GHz
- 펜티엄 D(2005): 3.2 GHz
- 쿼드코어 제온(2008): 3GHz
하지만 2000년대 중반부터는 하나의 칩에 들어있는 코어의 숫자가 성능의 주요 요소가 되었다. 듀얼 코어(2개), 쿼드 코어(4개), 옥타 코어(6개)처럼 코어의 숫자를 늘리는 데에 집중하게 되었다.
(교수님은 강의를 찍은 시점인 2011년에, 2020년이 되면 코어의 수가 2000개가 될 것이라고 예언했다. 하지만 2024년 현재도 CPU 코어의 숫자는 288개 내외를 유지하고 있다. 대신 계산에 최적화 된 GPU의 약진이 두드러진다!)
CPU의 대략적인 구조는 다음과 같다.
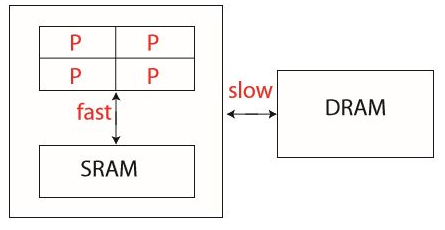
계산을 처리하는 프로세서(P)와 CPU내의 메모리(SRAM), 그리고 CPU 외부에 있는 메모리(DRAM)이 그림에 나타나 있다. P와 SRAM 사이의 데이터 교환은 매우 빠른 반면, 외부 메모리인 DRAM 사이의 교환은 비교적 느리다. 그러나, 코어의 숫자가 점점 늘어난다면 SRAM과의 교환에도 병목 현상이 발생하고, 속도가 느려지게 된다.
이를 해결하기 위해 캐시 메모리와 프로세서를 전부 병렬적으로 배치하는 아래와 같은 설계가 고안되었다.
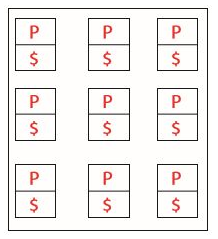
프로그램이 실행되는 대부분의 상황에서는 본인의 로컬 캐시 메모리에 접근하면 된다. 하지만 간혹 원격의 메모리에 접근해야할 때가 있다.
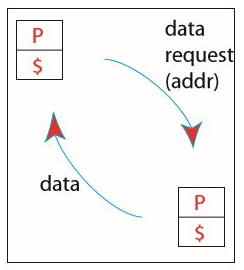
당연히 원격 접근의 속도를 향상시키는 것이 중요하고, 여기에는 최단 거리 알고리즘을 사용할 수 있다. 가중치는 회선의 혼잡도가 된다.
실행 이동
원격 접근 속도를 향상시키기 위해 새롭게 고안된 방법은 실행 이동(Execution Migration)이다. 기존에 원격 접근을 원하는 프로세서는 자신의 주소를 해당 메모리에 보내고 정보를 받는 방식으로 작동했다. 하지만 실행 이동에서는 자신의 문맥(context)을 다른 프로세서로 보내고 거기서 계산을 바로 하게끔 조치한다. 계산 결과나 데이터를 다시 돌려받을 필요가 없는 것이다!
위에서 살펴본 맥락은 다음과 같이 정의된다.
맥락 = 프로그램 카운터 + 레지스터 파일 + …
다만 실행 이동이 항상 좋지는 않다. 원격으로 데이터를 받는 것이 실행 이동으로 맥락을 옮기는 것보다 비용이 더 적을 수 있다. 그럼 지금부터는 실행 이동의 자세한 작동 방식과 그 복잡도를 알아본다.
프로그램의 접근 패턴을 알거나 예측할 수 있다고 가정하고, 메모리의 주소를 $m_1$, $m_2$, … , $m_N$, 각 메모리 주소의 프로세서 캐시를 $p(m_1)$, $p(m_2)$, … , $p(m_N)$ 라고 하자. 우리가 사용할 프로세서의 시퀀스를 $p_1 p_2 p_2 p_1 p_3 p_2$ 처럼 표현할 수 있다. 이동 비용과 접근 비용은 다음과 같이 정의된다.
- 이동 비용(s, d) = 거리(s, d) + L (적재 대기 시간)
- 접근 비용(s, d) = 2 $\cdot$ 거리(s, d)
s와 d가 같으면 비용은 0이다.
우리의 문제는 총 메모리 비용을 최소화하는 이동 시점을 계산하는 것이다. 다시 말해 언제 실행 이동을 하고 언제 원격 접속을 하는지를 결정하는 것이다.
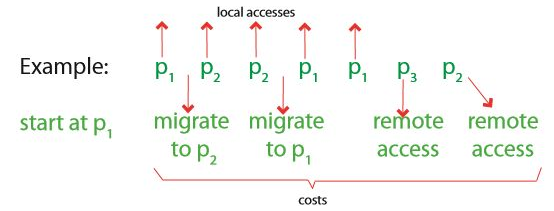
이 문제를 풀기 위해서 동적 프로그래밍을 사용한다!
프로그램의 최초 위치를 $p_1$, 프로세서의 개수를 Q라고 하자.
하위 문제는 DP(k, $p_i$)로 정의한다. 이는 프로그램이 $p_1$ 에서 시작해서 $p_i$ 에서 끝나는 경우, $m_1$ 에서 $m_k$ 까지의 메모리 접근의 prefix에 대한 최적해의 비용이다. 이는 두 가지 경우의 수(원격 접속, 실행 이동)가 있다.

하위 문제의 개수는 NQ개이다. 하위 문제당 시간은 O(Q)가 소요된다. 따라서 총 시간은 $O(NQ^2)$ 이다.
(교수님은 이 연구를 기반으로 128코어 프로세서를 설계하고 있다고 하셨다. 첫 128코어 프로세서 출시는 2020년이다. 상용화까지 9년 걸렸네…)
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기