계산 복잡도의 다양한 종류
계산 복잡도에는 다양한 종류가 있다.
- P = {다항 ($n^c$) 시간에 풀 수 있는 문제들}
- EXP = {지수 ($2^{n^{c}}$) 시간에 풀 수 있는 문제들}
- R = {유한 시간에 풀 수 있는 문제들}
가로축이 계산의 난이도라고 할 때, 계산 복잡도를 그래프로 나타낼 수 있다.
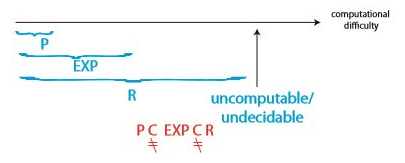
R보다 오른쪽에 있는 문제들은 계산이 불가능하거나 유한 시간안에 풀 수 없는 문제들이다.
각 문제들의 예시를 간단하게 살펴보자. 음수 가중치가 있는 사이클을 탐지하는 문제는 P에 해당하는 문제이다. 반면, (n x n) 체스의 승리 방법을 알아내는 문제는 EXP 문제이나, P에는 해당하지 않는다. 또한, 테트리스는 EXP 문제이며, P인지는 모른다.
정지문제는 컴퓨터 프로그램이 주어졌을 때 한 번이라도 정지하는지를 판단하는 문제이다. 이 문제를 풀 수 있는 알고리즘은 없으며, 계산이 불가능하다.
결정 문제는 대부분 계산 불가능이다.
결정 문제는 답이 ‘예’ 혹은 ‘아니오’로 결정되는 문제들이다. 우리가 앞서 봤던 예시들이 이에 해당한다. ‘음수 가중치가 있는가?’, ‘체스 경기에서 이길 방법이 있는가?’, ‘테트리스 게임이 해결 가능한가?’ 모두 결정 문제이다.
아주 충격적인 사실이지만, 결정 문제는 대부분 계산이 불가능한 문제들이다. 왜 그런지를 증명해보자.
우리의 컴퓨터 프로그램들은 이진 문자열이며, 이는 음이 아닌 정수(N)들이다. 그러나 결정 문제들은 이진 문자열을 예(1), 아니오(0)로 변환하는 함수로 볼 수 있으며, 이는 비트의 유한한 나열로 실수(R)들이다. 음이 아닌 정수는 실수보다 적으므로($\vert N \vert « \vert R \vert$) 우리가 아무리 많은 알고리즘(프로그램)을 만들더라도 모든 문제들을 해결할 수 없다. 이 얼마나 허무한가? 지금까지 우리는 무엇을 위해 알고리즘을 공부했는가?
우리가 푸는 문제들은 결정 문제들이고, 이는 결국 한 가지 종류의 문제라고 할 수 있다. 따라서 대부분의 문제들은 풀 수 없다.
NP
NP(비결정적 다항)는 다음과 같이 정의한다.
NP = {결정 문제는 ‘행운’ 알고리즘을 통해 다항 시간에 해결 가능}
NP는 비결정적 모델을 사용한다. 이 알고리즘은 추측을 하고 예, 아니오를 도출하는데, 여기서 추측은 동적 프로그래밍에서의 추측과 다르다. DP가 모든 추측을 다 시도하는 것과는 다르게, 행운 알고리즘은 항상 옳은 추측만을 한다. 닉값 만약 ‘예’로 귀결되는 해결책이 있다면 항상 그 해결책을 추측해내는 것이 보장된다. 다른 말로 하면 NP = {다항 시간에 확인될 수 있는 해답이 있는 결정 문제들} 이다.
가장 유명한(그리고 중요한) NP는 테트리스이다. ‘테트리스 게임에서 살아남았는가?’라는 질문에 대해 ‘예’라는 해결책이 있다면 그 움직임들의 리스트를 통해 해당 해결책을 증명할 수 있다.
앞서 본 그래프에 NP를 추가할 수 있다.
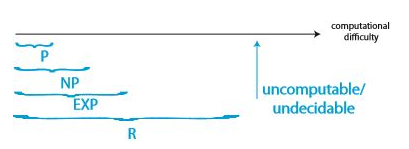
현재까지 정설은 P $\neq$ NP 이다. 분명 느꼈겠지만, 운에 의존하는 NP는 현실에서는 거의 구현하기 어렵다고 봐야한다. 우리는 운이 존재한다고 믿지만, 그렇다고 운을 설계하는 방법을 알지는 못한다. 비슷하게, 해답을 만드는 것은 그 해답이 맞는지를 증명하는 것보다 어렵다.
NP-완전, NP-난해
P $\neq$ NP 라면, 테트리스 문제 $\in$ NP - P 이다. 테트리스는 NP-난해 문제이기 때문이다. NP-난해(NP-hard)는 NP의 모든 문제들보다 적어도 더 어려운 문제이다. NP-완전(NP-complete)은 NP이면서 동시에 NP-난해인 문제(NP $\cap$ NP-난해)를 뜻한다. 그래프를 보면 더 잘 이해가 될 것이다.
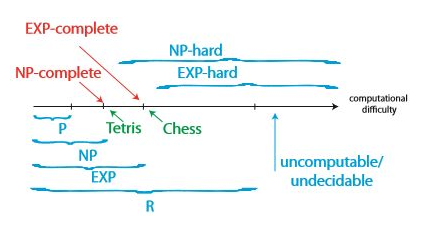
냅색 문제, 3-분할 문제(n개의 정수를 같은 합을 가지는 3개의 그룹으로 나누기), 외판원 문제, 지뢰 찾기, 공통 문자열, 3차원 최단 경로 등은 모두 NP-완전 문제이다.
비슷하게, 체스는 EXP-완전 문제이다.
리덕션
앞서 우리는 현실의 모든 문제를 알고리즘으로 해결할 수 없다고 했다. 그럼 그냥 포기해야 하나? 당연히 아니다! 해결할 수 없는 문제들을 해결할 수 있는 문제로 바꾸면 된다. 이를 리덕션이라고 한다. 다음은 리덕션의 몇 가지 예시이다.
| 현실 문제 | $\rightarrow$ | 바꾼 문제 | 방법 |
|---|---|---|---|
| 비가중치 최단 경로 | $\rightarrow$ | 가중치 최소 경로 | 모든 가중치를 1로 두기 |
| 최소 곱 경로 | $\rightarrow$ | 최단 경로 | 로그 취하기 |
| 최장 경로 | $\rightarrow$ | 최단 경로 | 가중치 음수 취하기 |
NP-완전 문제를 계속 리덕션 하다 보면 가장 마지막에 도달하는 지점은 어디일까? 논리식(and, or, not으로 이루어진 식)의 참 여부를 판별하는 SAT 문제에 도달한다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기