HJ

Leave HJ’s trace, All-In

지난 시간에 이어서 동적 프로그래밍의 5단계로 다양한 문제들을 해결해본다.

문자열 시퀀스 x에 대해 유용한 팁

문자열 시퀀스 x에 대해 DP를 적용할 때, suffix와 prefix 외에도 부분 문자열(substring)을 이용할 수 있다.

  • suffixes(x[i:]): 오른쪽에서 왼쪽으로 문제 해결. $\Theta(\vert x \vert)$.
  • prefixes(x[:i]): 왼쪽에서 오른쪽으로 문제 해결. $\Theta(\vert x \vert)$.
  • 부분 문자열(x[i:j]): $\Theta(x^2)$.

suffix와 prefix로도 모두 해결할 수 없으면 부분 문자열로 해결해야할 경우가 많다.


괄호 묶기

행렬의 곱셈은 결합 법칙만 성립하고 교환 법칙은 성립하지 않는다. 따라서 계산 횟수를 줄이려면 가장 먼저 계산할 부분을 잘 선택해야한다. 즉, 괄호를 잘 묶어야 한다. 예를 들어 다음과 같은 경우 계산 복잡도가 획기적으로 달라진다.

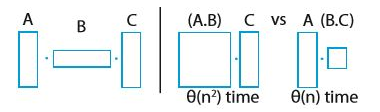
이 문제에 대해서는 추측을 먼저 하는 것이 도움이 된다.

  1. 추측
    가장 마지막에 할 곱셈을 선택해야 한다. 선택의 경우의 수는 $O(n)$ 이다.

  2. 하위 문제로 분류
    suffix도 아니고 prefix도 아닌 부분 문자열로 해결한다. 부분 문자열 A[i:j]의 비용을 구하는 것이 핵심인데, 하위 문제의 개수는 부분 문자열의 개수인 $\Theta(n^2)$ 가 된다.

  3. 재귀
    재귀 식은 ‘DP[i, j] = min(DP[i, k] + DP[k, j]) + (곱셈에 필요한 비용)’ 이 된다. 하위 문제당 비용은 어떨까? 곱셈에 상수 시간이 걸린다고 하면 1번에서 보았듯이 $O(j-i) = O(n)$ 이다. 가장 작은 단위는 무엇일까? DP[i, i+1]은 행렬 하나만을 의미하며, 비용은 0이다.

  4. 순서
    가장 작은 부분 문자열부터 문자열이 점점 커지는 순으로 계산하게 된다. 총 시간은 (늘 그랬듯이 공식을 사용해서) $O(n^3)$ 이다.

  5. 기존 문제
    DP[0, n]에 대해 계산하면 된다!

cf. 이 DP는 DAG의 최단 경로가 아니다. 이 문제를 DAG로 나타내면 두 개의 노드가 하나로 합쳐지는 방식으로 구현되므로, 이는 최단 경로에 대한 문제가 아니다.


편집 거리

두 개의 문자열 x, y에 대해, x를 y로 바꿀 때 가장 비용이 작은 편집 방법을 구하는 문제이다. 다음과 같은 예시가 있다.

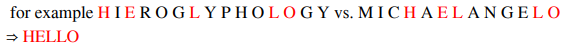
위 예시에서는 삭제만을 사용했지만 실제로는 3가지 방법이 있다. 문자열 삽입, 삭제, 교체가 그것이다.

cf. 이 문제는 생물학에서도 유용하게 사용할 수 있다. DNA의 염기 서열은 진화 과정에서 일부 변형되는데, 바뀌기 쉬운 변형이 있고(C에서 G로), 그렇지 않은 변형도 있다. 이 비용에 대한 계산을 통해 두 종의 진화적 거리를 계산할 수 있다.

가장 저렴한 편집 방법을 동적 프로그래밍으로 구해보자.

  1. 하위 문제로 분류
    하위 문제 c(i, j)를 x[i:], y[j:]에 대한 편집 거리라고 하자. 하위 문제의 개수는 x와 y의 문자열 길이만큼이므로 $\Theta(\vert x \vert \cdot \vert y \vert)$ 이다.

  2. 추측
    x를 y로 바꾸기 위해 다음과 같은 방법들을 생각해볼 수 있다. 이 3가지 밖에 없다.
    • x[i] 삭제
    • y[i] 삽입
    • x[i]를 y[i]로 교체
  3. 재귀
    2번의 추측으로부터 우리는 세 가지 방법에 대한 비용을 알아야 함을 깨달았다. 하나의 하위 문제 c(i, j)는 다음 값 중에 최솟값(min 연산)을 구해야 한다. 각 연산에 대한 비용에 다음 재귀 연산의 비용을 더한 것이다.
    • (x[i] 삭제 비용) + c(i + 1, j)
    • (y[i] 삽입 비용) + c(i, j + 1)
    • (x[i] $\rightarrow$ y[i] 교체 비용) + c(i + 1, j + 1)
  4. 순서
    2차원 표를 통해 직관적으로 이해할 수 있다. 아래에서 위로, 혹은 오른쪽에서 왼쪽으로 연산이 진행된다. 각 연산은 바로 우측, 바로 아래, 오른쪽 아래 대각선의 3개 칸에 대해서만 영향을 받는다(화살표로 표시됨). 3번에서의 모든 비용을 찾아내는 데 상수 시간이 걸린다고 하면, 총 시간은 $\Theta(\vert x \vert \cdot \vert y \vert)$ 이다.
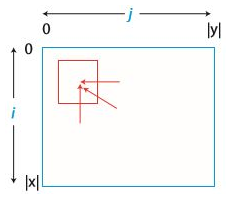
  1. 기존 문제
    c(0, 0)에 대해 계산하면 된다!


냅색 문제

약 1년 전 게시물 중에 동적 프로그래밍으로 냅색 문제를 다룬 적이 있다.

냅색 문제를 다룬 다른 게시물

쉽게 말해, 무인도에 갈 때 가져갈 물건을 고르는 문제라고 생각하면 된다. 가방의 크기는 한정되어 있고, 우리는 가치가 높은 물건들로만 가방을 꾸려서 가야 한다.

크기가 S인 가방에 짐을 넣는다. 물건 i는 크기 $s_i$ 와 가치 $v_i$ 를 가지고 있다. 가치를 최대로 하면서 크기의 합이 S를 넘어서는 안된다.

이 문제에서 조금 까다로움 부분은 물건의 크기 뿐만 아니라 가치도 고려해야한다는 것이다. 앞선 문제들에서 비용만을 최소화하면 OK였던 것과는 다르다.

  1. 하위 문제로 분류
    물건의 졍렬된 리스트가 있다고 할 때, 물건의 suffix를 확인할 수 있다. suffix [i:]의 가치를 판단하는 동시에 가방의 크기 S를 넘었는지를 판단하는 문제이다. 하위 문제의 개수는 물건의 개수 n에 크기 S를 곱한 $O(nS)$ 가 된다.

  2. 추측
    물건 i를 가져갈지 말지의 2가지 선택이 있다.

  3. 재귀
    재귀 식은 DP[i, X] = max(DP[i + 1, X], $v_i$ + DP(i + 1, X - $s_i$)) 이다. 우리는 물건 i를 가져가지 않는 경우(DP[i + 1, X])와 물건 i를 가져가는 대신 가방의 여분 공간이 줄어드는 경우(DP(i + 1, X - $s_i$)) 중에서 가장 가치가 높은 것을 선택해야 한다. 하위 문제 당 필요한 시간은 상수 시간이다.

  4. 순서
    suffix를 활용했기 때문에 오른쪽에서 왼쪽으로 가는 순서가 된다. 걸리는 총 시간은 $O(nS)$ 이다.

  5. 기존 문제
    DP[0, S]를 구한다.

이 문제의 총 시간 $O(nS)$ 은 다항시간일까? 아니다! 입력 값의 크기 n에 관한 다항식으로 표현되어야 다항시간인 것이다. S가 한 워드에 들어간다면 $\Theta(n)$ 이라고 할 수 있지만 일반적으로는 $O(n\log{S})$ 이다. 따라서 이 문제의 시간인 $O(nS)$ 는 $\log{S}$ 에 대해 지수적이므로 오히려 지수 시간이라고 할 수 있다. 이처럼 입력 값의 크기에 대한 다항식과 입력으로 받는 숫자들로 표현되는 시간을 ‘유사 다항 시간’이라고 한다.



별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기

참고