HJ

Leave HJ’s trace, All-In

알고리즘과 계산 모델

알고리즘은 컴퓨터 프로그램의 수학적 추상화라고 할 수 있다.


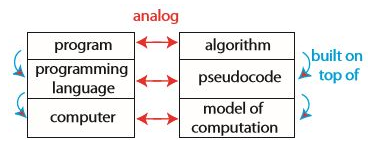
왼쪽이 컴퓨터, 오른쪽이 수학에 대응되는 항목들이다. 컴퓨터는 수학에서 계산 모델에 해당한다.

계산 모델은 알고리즘이 할 수 있는 연산, 각 연산의 비용, 알고리즘의 비용 등을 규정한다.


임의 접근 머신(RAM)



임의 접근 머신(Random Access Machine, RAM)은 거대한 배열로 이루어져 있다. 배열의 각 항목은 워드(word)이다. RAM에서 $\Theta(1)$ 의 시간 동안 할 수 있는 일은 다음과 같다.

  • 레지스터에 $r_i$에 있는 워드를 레지스터 $r_j$로 불러오기
  • 레지스터에서 연산(+, -, *, /, &, $\vert$, ^)
  • 레지스터 $r_j$를 $r_j$에 저장

여기서 워드는 그냥 w의 비트를 가진 것이라고 생각하면 된다. RAM은 불러오고, 계산하고, 저장하는 것에 거의 같은 시간($\Theta(1)$)이 소요된다는 특징이 있다.

저장장치 램과는 다르다


포인터 머신


포인터 머신의 예시인 이중 연결 리스트.


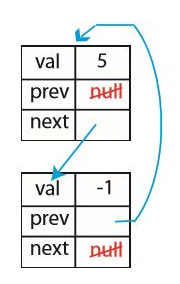
포인터 머신은 참조(reference)라고 생각하면 된다. 포인터 머신에는 RAM에는 없었던 동적 메모리 할당이 존재한다.

포인터 머신에는 포인터가 있는데, 포인터는 다른 객체를 가리키거나 null이라는 값을 가진다.

포인터를 따라가는 것, 필드를 바꾸는 것 등 일반적인 작업들은 모두 상수 시간이 소요된다.

포인터 머신은 RAM보다는 약하다.

파이썬에서는 네임드 튜플이나 속성이 여러 개 있는 객체가 포인터 머신이라고 할 수 있다.


파이썬 모델

파이썬에서는 RAM과 포인터 머신을 모두 구현할 수 있다. RAM은 리스트로, 포인터 머신은 O(1)개(상수)의 속성을 가진 객체로 말이다(속성은 너무 많지 않고 적당히 있어야 한다).

cf. 파이썬에서 리스트는 연결 리스트가 아니라 배열이다. 예를 들어 L[i] = L[j] + 5와 같은 연산을 할 때, $\Theta(1)$의 상수 시간이 소요된다. 만약 연결 리스트였다면 i 위치까지 훑어 가야하기 때문에 선형 시간이 소요됐을 것이다.

파이썬 리스트에서 하는 여러 가지 연산을 살펴보자.

  1. L.append(x)
    $\theta(1)$의 상수 시간이 소요된다. 흔히 리스트를 복사해서 한 칸을 늘리므로 선형 시간이 소요된다고 생각할 수 있지만, 파이썬은 ‘테이블 더블링’이라는 기법을 사용하기 때문에 상수 시간만이 걸린다.

  2. L = L1 + L2
    빈 리스트 L을 만들고($\theta(1)$), 반복문을 이용해 L1, L2의 요소들을 하나씩 더해주는 것($\theta(|L1|)$, $\theta(|L2|)$)으로 생각할 수 있다. 총 시간은 O(1 + L1의 길이 + L2의 길이)가 된다.

L = []

for x in L1:
    L.append(x)
for x in L2:
    L.append(x)

  1. in 연산 리스트에 요소가 들어있는지를 판단하는 in은 리스트를 훑어야 하므로 선형의 시간이 소요될 것이다.

  2. len(L) 여기서도 헷갈리기 쉽다. 선형 시간이 걸리는 것 아니냐고 말이다. 그러나 파이썬에서는 리스트를 만듦과 동시에 자신의 길이를 필드에 저장하기 때문에 그 값을 읽어오기만 하면 길이를 알 수 있다. 따라서 $\theta(1)$의 시간이 걸린다.

  3. L.sort() 파이썬에서는 비교 정렬을 사용한다. $\theta(\vert L\vert \log{\vert L \vert})$ 만큼의 시간이 걸린다.

튜플과 문자열, 집합은 리스트와 비슷하다.

딕셔너리는 가장 중요한 자료구조 가운데 하나이다. 해시 테이블이라고도 하는데, 나중에 다시 공부한다. 대부분의 연산은 $\theta(1)$ 의 시간이 소요된다.

heapq는 $\theta(\log{n})$ 의 시간이 소요된다.

정수 long 역시 나중 강의에서 다룬다고 한다. 간단하게만 살펴보면, $x + y$ 는 $O(\vert x \vert + \vert y\vert)$ 의 시간이, $x$ * $y$ 는 $O({\vert x \vert + \vert y \vert}^{\log{3}})$ 의 시간이 걸린다.


문서 거리 문제

학생들이 제출한 과제가 인터넷에서 배낀 것인지를 판단하고 싶다고 해보자. 그럼 우리는 문서 간의 유사도를 판별하는 알고리즘을 활용해야 할 것이다. 이를 ‘문서 거리 문제’라고 한다.

두 가지 사실을 정의하고 가자.

  • 단어: 영어와 숫자로 이루어진 문자열
  • 문서: 단어의 나열

유사도를 판별하는 가장 좋은 방법은 같은 단어가 얼마나 동시에 등장하는지를 파악하는 것이다. 문서 D를 벡터라고 생각하고, D[w]를 단어 w의 등장 횟수라고 해보자. 두 문서가 D1: “the cat”, D2: “the dog”라고 할 때, 공간에 두 벡터를 표현하면 다음과 같다.


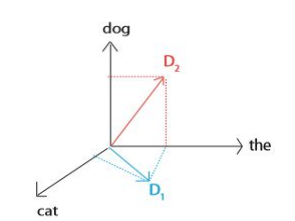
두 문서 사이의 거리를 어떻게 정의할까? 내적을 이용해볼 수 있다.

\[\displaystyle d'(D_1, \, D_2) = D_1 \cdot D_2 = \sum_{W}{D_1[W] \cdot D_2[W]}\]

이 방법의 문제는 문서의 규모에 따라 값의 크기가 달라져 유사도의 기준을 세울 수 없다는 것이다. 예를 들어 똑같이 유사도가 100%라고 해도, 문서의 길이가 50인 경우과 100인 경우 값의 크기가 다르다.

따라서 우리는 위 값을 단어의 개수로 나누어 줌으로써(정규화) 문제를 해결할 수 있다.

\[d''(D_1, \, D_2) = \frac{D_1 \cdot D_2}{|D_1| \cdot |D_2|}\]

그런데 어디서 많이 보지 않았는가? 이 값은 바로 두 벡터 사이의 각도($\cos{\theta}$)이다! 즉, 우리는 문서 사이의 거리를 각도를 이용해 표현한 것이다.

문서 거리 알고리즘을 정리하면 다음과 같다.

  1. 각 문서를 단어로 쪼갠다.
  2. 단어 빈도를 센다.
  3. 내적을 계산하고 나누어 각도를 구한다.

1번을 구현할 때는 정규표현식을, 2번을 구현할 때는 딕셔너리를 활용하면 된다. 주의할 점은 정규표현식의 re가 지수 시간이 걸린다는 점이다.

위 알고리즘의 최종 값이 1이면 동일한 문서이고, 0이면 아예 다른 문서일 것이다.



별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기

참고