동적 프로그래밍
동적 프로그래밍(Dynamic Programming, DP)은 하위 문제를 풀고(재귀), 그 결과를 재사용하는 방식의 알고리즘이다. ‘세심한 무차별 대입법(brute force)’이라고도 부르는데, 지수 시간이 걸리는 문제도 DP를 사용하면 다항 시간에 풀 수 있다.
다른 강의에서도 살펴봤지만 ‘동적 프로그래밍’이라는 용어는 해당 용어가 내포하는 의미와 잘 어울리지 않는다. DP를 개발한 리처드 벨만(‘벨만-포드’의 그 벨만 맞다)은 복잡한 것을 싫어하는 높으신 분들의 반발을 사지 않기 위해 친근하고 어렵지 않은 용어를 골라야만 했다. 그 결과 동적 프로그래밍이라는 용어가 탄생했다.
피보나치 수와 동적 프로그래밍
피보나치 수를 구하는 (아마도) 가장 유명한 방법은 재귀를 사용하는 것이다.
fib(n):
if n <= 2:
return f = 1
else:
return f = fib(n - 1) + fib(n - 2)
너무 유명하니 알고리즘 설명은 생략한다. 재귀적으로 계속 호출하기 때문에 당연히 시간 복잡도는 좋지 못하다. T(n)을 n번째 피보나치 수를 구하는 시간이라고 할 때, 다음과 같이 정리할 수 있다.
\[T(n) = T(n - 1) + T(n - 2) + O(1) \geq F_n \approx \phi^n \\ \geq 2T(n - 2) + O(1) \geq 2^{n/2}\]지수 시간이 걸리고 매우 나쁘다!
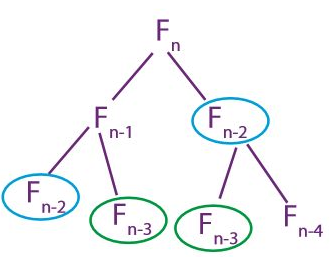
위 트리를 보면 재귀를 활용한 피보나치가 왜 나쁜지를 알 수 있다. 동일한 $F_{n-3}$ 이 몇 번이나 계산되는지를 보자! $F_{n-3}$ 이 나올 때마다 다시 계산하는 대신 한 번 계산하고 저장해두면 알고리즘을 좀 개선할 수 있을 것이다.
이처럼 계산 결과를 잠깐 메모하는 것을 메모이제이션(memoization)이라고 한다. 메모이제이션을 활용한 의사코드를 보자.
memo = {}
fib(n):
if n in memo:
return memo[n]
else:
if n <= 2:
return f = 1
else:
return f = fib(n - 1) + fib(n - 2)
memo[n] = f
return f
memo 딕셔너리에 중간 계산 결과를 저장해놓는다. fib(k)는 처음 호출될 때만 재귀 호출 되며, 이후부터는 거의 공짜 시간(상수 시간)에 계산 결과를 가져다 쓸 수 있다. 재귀를 무시한다면 호출당 $\Theta(1)$ 의 시간이 걸린다.
DP는 재귀와 메모이제이션을 합친 것으로 볼 수 있다. 문제를 하위 문제로 나누고, 하위 문제의 답을 재사용하는 방식으로 큰 문제를 해결한다. 걸리는 소요 시간은 하위 문제의 개수와 하위 문제당 소요 시간을 곱한 것이다.
(소요 시간) = (하위 문제의 수) $\cdot$ (하위 문제당 소요 시간)
피보나치의 경우에는 $\Theta(1) \cdot n = \Theta(n)$ 의 시간이 걸린다.
상향식 DP 알고리즘
근데 굳이 재귀 함수를 사용해야할까? 재귀를 사용하지 않고도 자료구조만 잘 활용하면 피보나치 수를 구할 수 있다.
fib = {}
for k in range(1, n + 1):
if k <= 2:
f = 1
else:
f = fib[k - 1] + fib[k - 2]
fib[k] = f
return fib[n]
fib 딕셔너리에 계산된 피보나치 수를 계속해서 업데이트 하고, 이를 그냥 가져다 쓰는 것이다. 재귀를 ‘펼쳐서’ 계산했다고도 볼 수 있다. 하위 문제 종속 방향성 비순환 그래프의 위상정렬로도 생각할 수 있다.
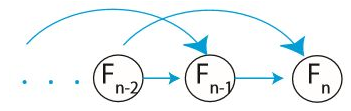
이전 두 피보나치 수만을 기억하므로 공간을 절약할 수 있고, 재귀가 없기 때문에 더 빠르다.
최단 경로와 동적 프로그래밍
최단 경로를 구하는 데에도 DP를 사용할 수 있다. 앞서 DP를 세심한 무차별 대입법이라고 했을 것이다. 마찬가지로 최단 경로 계산에 DP를 적용하는 것은 모든 값을 시도해보는 추측(guess)의 방법이다.

s에서 v까지의 최단 경로를 계산한다고 해보자. 경로에서 마지막 간선은 알 수 없으므로 (u, v)라고 추측한다. 그렇다면 최단 경로는 ‘(s에서 u까지의 최단 경로) + (u, v)’ 가 된다. 비용은 $\delta _{k-1}(s, u) + w(u, v)$ 가 된다. 이제 s에서 u까지의 최단 경로를 구하는 하위 문제가 생겼다. 이제 피보나치 수를 구하듯이 계속 하위 경로를 만들면서 최단 경로를 찾으면 된다!(…)
물론 이 자체로는 매우 나쁜 방법이다. 다만 메모이제이션을 사용하면 조금 낫다. 이제 우리가 알고 있는 DP는 재귀, 메모이제이션, 추측을 합친 것이다!
근데 이 방법에는 치명적인 결함이 있다. 만약 그래프에 순환이 있다면? 재귀 과정에서 우리가 구하고자 하는 경로가 하위 문제로 다시 등장하게 되고, 이를 또 재귀적으로 구하다보면 결국 무한 시간이 걸릴 것이다. (마치 경찰서와 소방서의 위치를 모르는 사람에게 경찰서는 소방서 옆에 있고, 소방서는 경찰서 옆에 있다고 설명하는 꼴이다.)
이를 해결하기 위해서는 하위 문제 종속이 비순환적이어야 한다. 그래프를 비순환으로 바꾸는 방법은 다음과 같다.
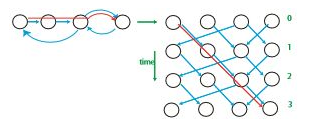
그래프를 상하 축을 기준으로 쭉 복제한 것이다. 상하 축은 시간을 나타낸다. 이제 그래프가 방향성 비순환 그래프가 되었다. 이렇게 하면 소요 시간은 (동적 프로그래밍 소요 시간 공식을 활용해서) $\displaystyle \Theta(V \sum_{v \in V}{indegree(V)}) = \Theta(VE)$ 가 된다 (indegree는 외부 노드에서 들어오는 간선의 수). 벨만-포드 알고리즘의 소요 시간과 동일하다!
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기