이번 시간에 배울 모든 내용은 실제 현실에 적용했을 때 성능이 더 증가하는 방법들이다. 따라서 완벽한 증명보다는 직관적인 이해가 조금 더 도움이 될 수 있다. 나는 그랬다
단일 시작 단일 도착 다익스트라
만약 우리가 모든 점에 대한 최단거리 정보가 아니라 s에서 t까지의 최단거리만 필요하다면 더 빠르게 원하는 것을 찾을 수 있다.

다른 모든 과정은 동일하지만 u = t 일때 종료하는 조건이 추가되었다. 우선순위 큐에서 t가 제거되었을 때 알고리즘을 종료하는 것이다. 그러면 우리는 s에서 t로부터의 최단거리를 모든 정점에 대해 계산하는 것보다 더 수월하게 구할 수 있다. 또한, t가 가장 마지막의 정점이더라도 기존 알고리즘보다 더 늦어지지 않는다.
양방향 탐색
양방향 탐색은 말 그대로 양쪽에서 동시에 탐색해나가는 것이다. 기본적으로 아래와 같은 아이디어로 진행된다.
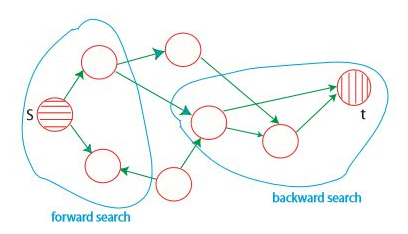
기존에 하던 방식대로 시작점에서 도착점으로 탐색하는 것을 정방향 탐색(forward search), 반대로 도착점에서 출발점으로 탐색하는 것을 역방향 탐색(backward search)라고 한다. 양방향 탐색에서는 정방향 탐색 1회, 역방향 탐색 1회를 번갈아가며 진행한다. 양방향 탐색은 복잡도를 바꾸지는 않지만 실제 적용했을 때 방문하는 정점의 수를 줄이는 효과가 있다.

양방향 탐색 알고리즘은 위와 같다. $d_f(u)$ 는 정방향 탐색에서의 거리, $d_b(u)$ 는 역방향 탐색에서의 거리이다. 비슷한 맥락으로, $\Pi _f(u)$ 는 정방향 탐색에서의 선행자, $\Pi _b(u)$ 는 역방향 탐색에서의 선행자이다. 예를 들어, $d_f(s) = 0$, $\Pi _f(v_1) = s$, $\Pi _b(v_2) = t$ 이다.
양방향 탐색에서 종료 조건은 무엇일까? 직관적으로 생각해보면 정방향 탐색을 통해 생기는 경계와 역방향 탐색으로 생기는 경계가 만나는 지점일 것이다. 그러나 우리는 의사 코드로 표현할 수 있을 정도로 정형화된 표현이 필요하다. 더 제대로 된 종료 조건은 ‘어떤 정점 w가 정방향 큐($Q_f$)와 역방향 큐($Q_b$) 모두에서 제거되었을 때’이다. 큐에서 제거되었다는 것은 최단 거리 경로로 탐색되었다는 것이고, 이는 곧 경계에 포함되었다는 의미이니 적절해보인다.
양방향 탐색으로 최단 경로는 어떻게 찾을까? w까지의 정뱡향, 역방향 거리를 더한 $d_f(w) + d_b(w)$ 일까? 다음 예시를 보자.
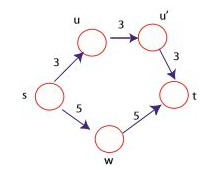
s에서 t까지의 최단거리는 u와 u’를 지나는 경로(가중치 9)이다. 이제 양방향 탐색으로 최단 경로를 찾아보자.
일단 정방향 탐색을 1회 진행한다.
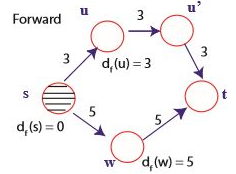
정방향 탐색이 완료된 정점은 가로 빗금으로 표시된다. 정방향 탐색을 했으니 역방향 탐색도 1회 해주어야 한다.
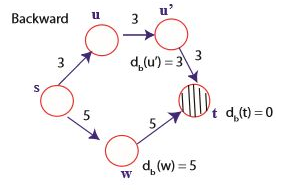
역방향 탐색이 완료되면 세로 빗금으로 표시된다. 다음으로 정방향 탐색을 하면, u의 우선순위가 더 작으므로 u가 탐색될 것이다.
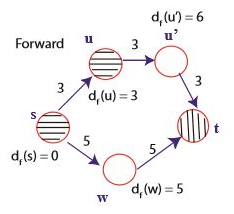
역방향 탐색에서는 u’의 우선순위가 더 작으므로 u’이 탐색된다.
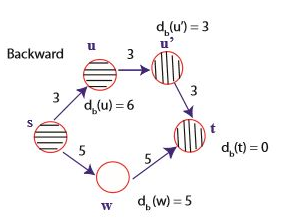
다음 정방향 탐색에서는 $d_f(u^{\prime})$ 와 $d_f(w)$ 가 비교된다. w의 우선순위가 더 작으므로 w로 탐색한다.
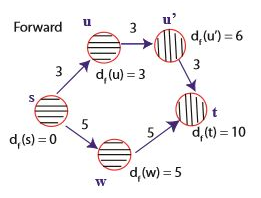
역방향 탐색에서는 $d_b(u)$ 와 $d_b(w)$ 를 비교해서 w로 탐색할 것이다.
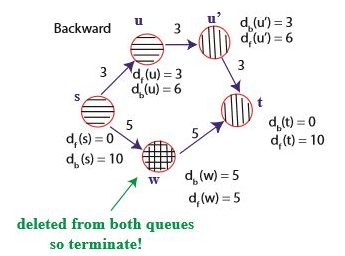
w가 $Q_f$, $Q_b$ 모두에서 제거되었으므로 알고리즘이 종료된다. 그런데 $d_f(w) + d_b(w)$ 로 최단거리를 계산하면 가중치가 10으로, 정답이 아니다! 양방향 탐색에서는 정방향과 역방향을 1회씩 반복하므로 간선의 수가 가장 적은 경로를 최단 경로라고 할 수 밖에 없다. 이처럼 경계가 만나는 정점을 기준으로 최단 경로를 구하면 오류가 발생할 수 있다.
양방향 탐색에서 최단 경로를 찾는 더 나은 방법은 한 번의 탐색에서 처리된 모든 정점 x에 대해 $d_f(x) + d_b(x)$ 를 구하는 것이다.
$d_f(u) + d_b(u) = 3 + 6 = 9$
$d_f(u^{\prime}) + d_b(u^{\prime}) = 6 + 3 = 9$
$d_f(w) + d_b(w) = 5 + 5 = 10$
이제 우리는 양방향 탐색으로 최단 경로도 구할 수 있다.
목적 지향 탐색
포텐셜 함수($\lambda$)로 간선의 가중치를 수정할 수 있다.
\[\overline{w}(u, v) = w(u, v) - \lambda(u) + \lambda(v)\]잘 설정된 포텐셜 함수로 가중치를 수정하면 간선의 포텐셜을 조정할 수 있고, 최단 경로에 해당하는 간선의 포텐셜을 낮추어 더 빠르게 최단 경로를 탐색하도록 도울 수 있다.
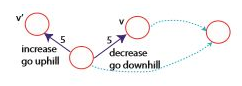
가중치 $\overline{w}(u, v)$ 로 수정된 그래프에서도 최단 경로는 바뀌지 않아야 한다. 이러한 수정의 한 가지 예시는 다음과 같다.
\[\overline{w}(p) = w(p) - \lambda _t(s) + \lambda _t(t)\]모든 가중치가 평행이동하는 것과 다름이 없으므로 최단 경로는 바뀌지 않는다.
포텐셜 함수를 구하는 한 가지 방법은 랜드마크를 이용하는 것이다. 랜드마크는 그래프 위의 한 정점이다. 한 정점을 랜드마크 $l$ 로 지정하고, 모든 정점 u에 대해 $\delta(u, l)$ 을 미리 계산한다. 잠재력 함수는 다음과 같다.
\[\lambda _t^{(l)}(u) = \delta(u, l) - \delta(u, l)\]$\delta(u, l)$ 은 u가 다양하므로 여러 번 계산해야하지만, $\delta(u, l)$ 는 도착점 t에 대해 한 번만 계산하면 된다. 위 잠재력 함수는 삼각 부등식에 의해 잘 작동됨이 증명되지만 직관적으로 이해해볼 수도 있다. 서울에서 부산까지의 최단 경로를 구할 때, 그 중간에 있는 대구를 지날 가능성이 높으므로 대구를 랜드마크로 설정하는 것이다. 그럼 서울에서 부산까지의 최단 경로를 조금 더 수월하게 구할 수 있을 것이다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기