일반적인 최단 경로 알고리즘의 문제점
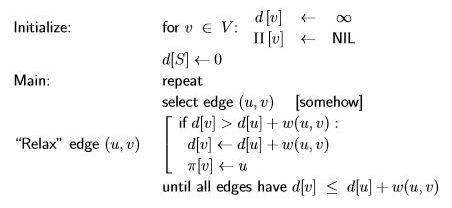
일반적인 최단 경로 알고리즘은 위와 같은데, 2가지 문제점이 있었다.
- 간선을 선택하는 순서에 따라 완화를 지수 시간만큼 해야함. (다익스트라 알고리즘으로 해결)
- 음의 순환이 있으면 사용 불가.
벨만-포드 알고리즘으로 음의 순환을 해결할 수 있다.
벨만-포드 알고리즘
이 강의를 들은지 5년이 지나면 아무 것도 기억이 나지 않겠지만, 그럼에도 반드시 기억해야 하는 사실이 있다. 다항 시간이 걸리는 알고리즘은 좋으며, 지수 시간이 걸리는 것은 나쁘고, 무한대의 시간이 걸리면 직장에서 해고될 것이다.
벨만-포드 알고리즘은 다음과 같다.
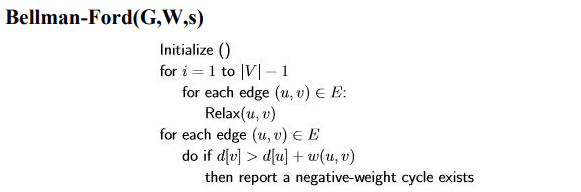
초기화 과정에서는 $d[s] = 0$, 나머지는 $\infty$ 로 설정한다. 첫 번째 반복문은 완화 과정을 나타낸다. $(\vert V \vert - 1)$ 번 반복하는데, 각 반복에서 모든 간선을 한 번씩 완화한다. 만약 그래프에 음의 순환이 없다면 $(\vert V \vert - 1)$ 번의 반복으로 최단 경로를 찾을 수 있다 (증명은 나중에 한다). 주목할 것은 한 번 반복할 때마다 모든 간선을 완화한다는 점이다.
그 다음 반복문은 음의 순환 여부를 체크하기 위한 것이다. $d[v] > d[u] + w(u, v)$ 라면 음의 순환이 있다는 뜻이므로 음의 순환이 있다고 보고한다.
시간 복잡도는 어떻게 될까? 첫 번째 반복문은 $O(VE)$, 두 번째 반복문은 $O(E)$ 이므로, $O(VE) + O(E) = O(VE) = O(V^3)$ 가 된다.
벨만-포드 알고리즘 관련 정리
정리: 그래프 (G, E)가 음의 순환을 가지고 있지 않으면, 벨만-포드 알고리즘 종료 후 모든 그래프의 정점 $v \in V$ 에 대해 $d[v] = \delta(s, v)$ 이다.
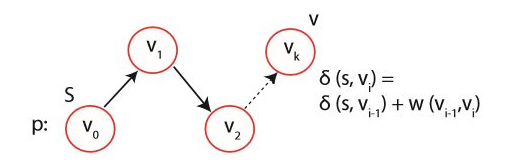
증명은 간단하다. $v \in V$ 를 그래프 내의 정점이라고 하고, $v_0 = s$ 에서 $v_k = v$ 까지의 경로 $p = <v_0, v_1, …, v_k>$ 를 ‘최소 개수의 간선을 가진 최단 경로’라고 둔다. 음의 순환이 없다면 p는 단순 경로가 된다. p가 단순 경로라면, 최단 경로로 갈 때 거치는 정점의 개수는 전체보다 작거나 같으므로 $k \leq \vert V \vert -1$ 이다.
이제 귀납적으로 증명하면 된다. $d[v_0] = \delta(s, v_0) = 0$ 이고, 음의 순환이 없으므로 이 값은 변하지 않는다. 벨만-포드 알고리즘에 의해 모든 간선 E에 대해 첫 번째 완화를 했다고 하자. 그럼 $(v_0, v_1)$ 이 완화되고, $d[v_1] = \delta(s, v_1)$ 가 된다. 이는 모든 간선에 대해 완화를 했을 때 더 짧은 경로를 찾을 수 없기 때문이다(우리는 애초에 p를 최단 경로로 선택했다. 최단 경로의 부분은 최단 경로이다!). 모든 간선 E에 대해 완화를 또 하면 $(v_1, v_2)$ 이 완화되고, $d[v_2] = \delta(s, v_2)$ 가 된다. 모든 간선 E에 대해 i번 완화를 하면 $d[v_i] = \delta(s, v_i)$ 가 된다. 따라서, $(k \leq \vert V \vert - 1)$ 번의 완화를 하면 $d[v_k] = \delta(s, v_k)$ 를 얻을 수 있다.
벨만-포드 알고리즘 관련 따름 정리
따름 정리: $(\vert V \vert -1)$ 번의 완화 과정 이후에도 d[v]의 값이 수렴하지 않으면 s로부터 도달할 수 있는 음의 순환이 존재한다.
$(\vert V \vert -1)$ 번의 완화 과정 이후에도 완화될 수 있는 간선이 있다면, 이는 같은 정점을 중복 방문한다는 의미이다. 즉, 순환을 포함하는 경로가 우리가 찾은 현재 최단 경로보다 가중치가 작으므로, 음의 순환을 가진다.
최장 단순 경로 구하기
지금까지 배운 알고리즘으로 가중치의 합이 가장 큰 최장 단순 경로를 찾을 수 있을까? 양의 가중치만을 가진 그래프의 모든 가중치를 음수로 바꾸고, 벨만-포드 알고리즘을 적용하면 될 것 같기도 하다.
그러나 이는 매우 어려운 문제이다. 벨만-포드 알고리즘은 음의 순환을 발견하면 바로 종료되기 때문에 실질적으로 최장 경로를 ‘계산’하는 것은 불가능하다. 쉽게 말해, 음의 순환을 감지만 할 뿐 대안을 제시하지는 못한다.
최장 단순 경로, 최단 단순 경로를 실질적으로 구하는 것은 모두 NP-hard 문제이다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기