완화의 안전성
최적 경로를 계속 업데이트 하는 과정인 완화는 안전한(정당한) 과정이다. 증명을 위해서는 다음과 같은 보조 정리를 활용한다.
보조 정리: 완화 알고리즘은 불변 조건인 모든 $v \in V$ 에서 $d[v] \geq \delta(s, v)$ 임을 항상 만족한다.
증명은 귀납법으로 한다. 귀납법에 의해 $d[u] \geq \delta(s, u)$ 이라고 가정한 뒤, 삼각 부등식 $\delta(s, v) \leq \delta(s, u) + \delta(u, v)$ 을 변형해보자. $d[u] \geq \delta(s, u)$ 이고 $w(u, v) \geq \delta(u, v)$ 이므로 $\delta(s, v) \leq d[u] + w(u, v)$ 가 된다. 그러므로, $d[v] = d[u] + w(u, v)$ 로 할당하는 것은 안전하다.
DAG에서의 최단 경로 계산
방향이 있는 비순환성 그래프(Directed Acycle Graph, DAG)에서 최단 경로는 다음과 같이 구한다.
- DAG를 위상 정렬한다.
- 위상 정렬된 정점을 한 번 훑으면서 그 정점에서 나가는 간선에 대해 완화한다.
위 과정은 출발점을 정해주지 않는다. DAG를 위상 정렬하면 출발지로 설정할만한 곳들이 보일 것이다.
예시를 통해 이해해보자.
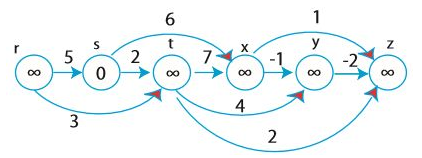
왼쪽에서 오른쪽으로 위상 정렬된 상태이다. s를 출발점으로 한 뒤, 모든 점들의 d값을 $\infty$ 로 설정하였다.
그 다음에는 s에서 나가는 간선에 위치한 정점에 대해 완화를 실시한다. t와 x가 그 대상이 된다.
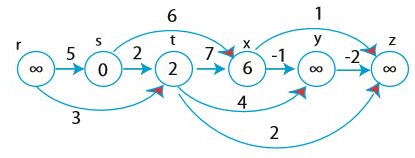
s에 대해서는 끝났으니, 이제 t, x, y에 대해 완화를 해준다.
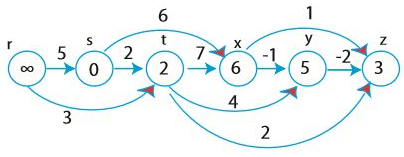
r은 출발점 s보다 왼쪽에 위치하므로 $\infty$ 를 유지한다.
이 방법은 DAG에 대해서만 사용 가능하다.
다익스트라 알고리즘
이 부분을 시작할 때 교수님은 공과 실을 이용해 다익스트라 방법을 물리적으로 입증했다. 간선을 가중치에 비례하는 길이의 실로 두고 시작점에 해당하는 공을 가장 위로 들면 최단 거리 순서대로 정렬이 된다.
다익스트라 알고리즘은 모든 가중치가 0 이상일 때만 사용할 수 있다. 각 간선 $(u, v) \in E$ 에 대하여, 정점의 집합 S에 최단 경로의 값이 결정된 정점만을 넣는다. 최단 경로 예측값을 가지는 u를 V-S 집합(아직 최단 경로가 결정되지 않은 집합)에서 반복적으로 선택하여, u를 S에 넣고(최단 경로 값을 결정하고), u로부터 나가는 모든 간선에 대해 완화한다.
한 번에 이해가 안될 수 있다. 2번 이상 천천히 읽어보자.
의사 코드를 살펴보자.

여기서 Q는 우선순위 큐(priority queue)이다.
코드를 보기 전에 설명한 다익스트라 알고리즘의 흐름을 이해했다면 코드 역시 이해하기 어렵지 않다. EXTRACT-MIN(Q)는 Q에서 가장 우선순위가 작은(현재 가장 가까운) 점을 추출하라는 뜻이다.
아직도 이해가 어렵다면 예시를 통해 이해해보자.
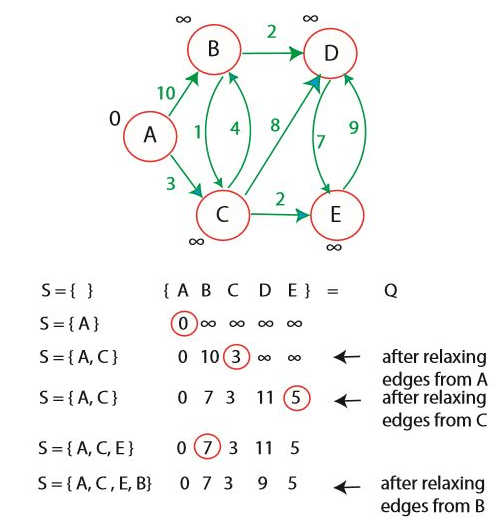
S는 처음에 비어있다. 우선순위 큐 Q에서 A의 우선순위가 가장 작으므로 A를 S에 넣는다. 그리고 A에서 나가는 간선에 위치한 B, C의 d값을 조정한다. 그 다음 우선순위가 작은 것은 C이므로 C가 S에 들어간다. 그리고 다시 C에서 나가는 간선에 위치한 정점들의 d값을 조정한다. 이때, A와 C는 이미 최단 거리를 찾은 상태로, 다시 건드리지 않는다. 이 과정을 S에 들어가지 못한 정점이 더 이상 없을 때까지 반복한다.
다익스트라 알고리즘은 탐욕 알고리즘이다. V-S에서 가장 가까운 정점을 선택하기 때문이다.
다익스트라 알고리즘에서 시간 복잡도는 어떻게 될까? 먼저,
- $\Theta(V)$ 번의 우선순위 큐 삽입 연산
- $\Theta(V)$ 번의 EXTRACT-MIN 연산
- $\Theta(E)$ 번의 DECREASE-KEY 연산
이 있다.
그 다음 과정부터는 큐에 어떤 자료구조를 사용하는지에 따라 달라진다. 배열을 사용하면 다음과 같다.
- $\Theta(V)$: 최소의 원소(EXTRACT-MIN) 추출
- $\Theta(1)$: DECREASE-KEY 연산
결론적으로는 $\Theta(V \cdot V + E \cdot 1) = \Theta(V^2 + E) = \Theta(V^2) \quad (E = V^2)$ 이다.
이진 최소 힙을 사용하면 조금 달라진다.
- $\Theta(\log{V})$: 최소의 원소(EXTRACT-MIN) 추출
- $\Theta(\log{V})$: DECREASE-KEY 연산
최소 원소 추출은 배열보다 낫지만, DECREASE-KEY 연산이 나빠져서 결과적으로는 $\Theta(V\log{V} + E\log{V})$ 가 된다.
그러나 이러한 자료구조들은 다익스트라 알고리즘의 최소 시간에 도달하지 못한다. 우선순위 큐에는 피보나치 힙을 사용하면 가장 좋다.
- $\Theta(\log{V})$: 최소의 원소(EXTRACT-MIN) 추출
- $\Theta(1)$: DECREASE-KEY 연산
- 분할상환 비용
최소 원소 추출, DECREASE-KEY 연산 모두 더 좋아졌다. 궁극적으로 $\Theta(V\log{V} + E)$ 가 된다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기