본 게시글에서는 네이버 부스트코스의 해석을 참고하여 가중치가 가장 작은 경로를 ‘최단 경로’라고 표현하였다.
최단 경로 찾기 문제
최단 경로 문제에서 사용되는 그래프는 $G(V, E, W)$ 로 표현할 수 있다. 여기서 V는 정점, E는 간선이고, W는 간선이 가지고 있는 가중치($W: E \rightarrow R$)이다.
최단 경로를 찾는 것에는 두 가지 알고리즘을 사용할 수 있다.
- 다익스트라: 가중치가 음이 아닐 때 사용한다. $O(V\log{V} + E)$ 의 복잡도를 가진다.
- 벨만-포드: 가중치의 부호와 관계 없이 사용 가능하다. $O(VE)$ 의 복잡도를 가진다.
정점들이 모두 간선으로 연결된 완전 그래프에서는 $E=O(V^2)$ 의 관계를 가진다. 즉, 벨만-포드 알고리즘의 복잡도는 $O(V^3)$ 가 되며, 매우 비효율적이다. 따라서 다익스트라 알고리즘을 쓸 수 있다면 다익스트라를 쓰는 것이 좋다.
최단 경로를 찾는 문제는 다음과 같이 정의된다.
경로 p = <$v_0$, $v_1$, …, $v_k$>
($v_k$, $v_{k+1}$) $\in E$ for $0 \leq i < k$
$\displaystyle w(p) = \sum_{i=0}^{k-1}{w(v_i, v_{i+1})}$
간선 $(v_i, v_{i+1})$ 의 가중치인 $w(v_i, v_{i+1})$ 의 합을 최소화하는 경로 p를 찾는 것이 우리의 목표이다.
가중치는 $E^2$개가 가능하다. 다만, 그 범위는 정해져 있지 않다. 어차피 복잡도는 W에 대한 함수가 아니기 때문에, 가중치의 범위가 없다고 해도 복잡도에 끼치는 영향은 없다.
양의 가중치 간선
$v_0$ 에서 $v_k$ 까지의 경로 p는 다음과 같이 표현한다.
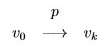
$(v_0)$ 은 $v_0$ 에서 $v_0$ 까지의 가중치가 0인 경로를 의미한다.
u에서 v까지 최단 경로의 가중치를 다음과 같이 정의한다.
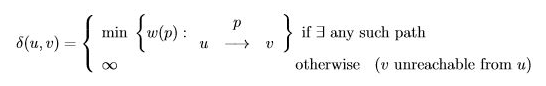
$\delta(u, v)$ 가 u에서 v까지의 최단 경로의 가중치이다. 이는 u에서 v까지의 경로 중에 가중치가 가장 작은 것을 선택하면 되지만, 만약 그게 없다면 그냥 $\infty$ 가 된다.
그럼 이제 예시에서 가중치가 가장 작은 경로를 찾아보자.
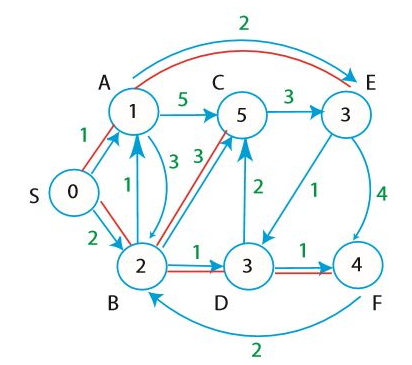
S에서 A로 가는 경로는 한 가지 뿐이다. $\delta(S, A) = 1$ 가 된다. $\delta(S, C)$ 는 어떨까? 1에 $w(A, C)=5$ 를 더해야 하므로 6이라고 생각할 수 있다. 근데 틀렸다! S에서 출발해 B를 거쳐서 C로 가는 것이 가중치가 더 작다. 따라서 $\delta(S, A) = 5$ 가 된다. 이처럼 계속해서 값을 업데이트하면서 최단 경로를 찾으면 된다.
거쳐온 정점의 수가 적다고 가중치가 적은 것이 아니다! 거쳐온 정점이 아무리 많아도 그들의 가중치가 매우 작다면, 가중치가 큰 정점 몇 개를 거친 것보다 더 나을 수 있다.
몇 가지 표현을 약속하고 가자. $d[v]$는 v로 가는 최소 가중치의 현재 값이다. 즉, 이 값은 더 나은 경로를 찾으면 업데이트 될 수 있다. 마치 우리가 $\delta(S, C) = 6$ 이라고 생각했다가($d[C] = 6$), $\delta(S, C) = 5$ 로 바꾼 것($d[C] = 5$)처럼 말이다. $\Pi[v]$ 는 v로 가는 최단 경로에서 v 직전에 등장하는 정점이다.
음의 가중치 간선
가중치가 음인 경우도 있을까? 만약 우리가 운전을 하는데, 특정 경로를 통과하면 통행료를 지불하는 것이 아니라 오하려 운전비를 받는다고 해보자. 그럼 이 경우는 음의 가중치가 아니면 표현할 방법이 없을 것이다.
몇몇 경우는 음의 가중치로도 표현할 수 있고 양의 가중치로도 표현할 수 있다. 앞서도 말했듯이, 다익스트라 알고리즘을 사용할 수 있는 경우(양의 가중치)라면 최대한 양의 가중치로만 표현하는 것이 좋다.
음의 가중치를 가진 그래프에서 주의해야할 것은 음의 사이클이다. 아래 예시를 보자.
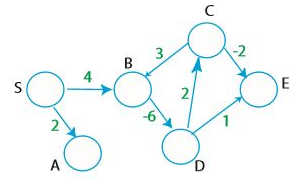
B, C, D의 사이클을 주목해보자. 이 가중치를 모두 더하면 -1이 된다. 즉, 이 사이클을 무한 반복하면 가중치를 계속 줄여나갈 수 있기 때문에 $\delta(A, B)$를 찾는다면 알고리즘이 끝나지 않을 수 있다. 이를 해결하기 위해서는 우리의 알고리즘이 음의 사이클을 발견할 수 있어야 한다. 벨만-포드 알고리즘이 이 역할을 해주며, 나중에 더 자세히 알아본다.
일단 음의 사이클이 없을 때의 알고리즘을 정리해보자.
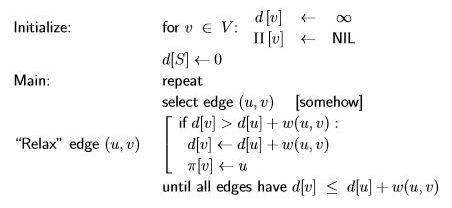
랜덤하게 간선을 선택하고, 완화(relax)라는 과정을 통해 이를 검증해서 최단 경로를 찾는 것으로 이해하면 된다. 완화 과정에 주목해보면, 기존의 방법보다 더 나은 방법을 찾았을 때 $d[v]$ 와 $\Pi[v]$ 를 업데이트 한다. 그리고 모든 간선이 $d[v] \leq d[u] + w(u, v)$ 의 조건을 만족하면 알고리즘을 종료한다. 이 조건은 모든 간선에 대한 것이므로 O(E) 번의 체크가 필요하다. 즉, 위 알고리즘은 잘 작동하긴 하지만 매우 느리다.
간선을 선택하는 순서가 중요한 이유
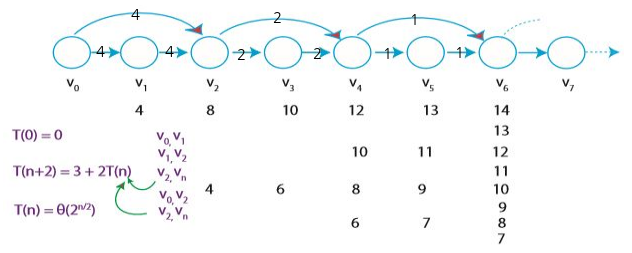
위 그래프에서 최단 경로를 찾는 중이라고 해보자. $d[V_6]$ 를 업데이트 하는 과정이 여러 번 진행되어 매우 지저분한 것을 볼 수 있다. 왜 그럴까? 이는 간선을 선택하는 순서가 잘못되었기 때문이다. 이처럼 간선을 선택하는 순서 역시 매우 중요하다.
최적 부분 구조
두 가지 정리에 대해 살펴본다.
- 정리 1: 최단 경로의 부분 경로는 최단 경로이다.
증명은 간단하다.
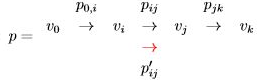
만약 위 최단 경로 p로 향하는 과정에 없는 $p_{ij}^{\prime}$ 가 $p_{ij}$ 보다 작다고 하면, $p_{ij}^{\prime}$ 를 사용할 때가 기존의 p보다 작아진다. 이는 모순이다.
- 정리 2: 모든 $u, v, x \in X$ 에 대해, $\delta(u, v) \leq \delta(u, x) + \delta(x, v)$ 이다. (삼각 부등식)
역시 증명은 어렵지 않다.
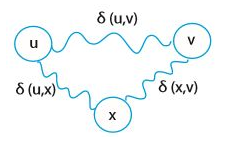
$\delta(u, v) > \delta(u, x) + \delta(x, v)$ 라고 하면, u에서 v로 가는 최단 경로는 (u, v)가 아니라 x를 거쳐가는 길이 되고, $\delta(u, x) + \delta(x, v) = \delta(u, v)$ 가 되어버린다. 모순이 발생하는 것이다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기