그래프
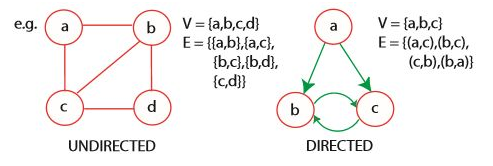
그래프는 정점(V)과 정점을 잇는 간선(E)으로 이루어지며, G = (V, E) 와 같이 표현할 수 있다. 그래프는 방향의 유무에 따라 방향이 있는 그래프(directed)와 방향이 없는 그래프(undirected)로 나뉜다.
그래프를 탐색한다는 것은 그래프의 시작점 s에서 도달할 수 있는 모든 정점과 간선을 방문해서 특정 정점까지의 경로를 찾는다는 뜻이다. 이는 선형의 시간이 걸린다.
그래프와 그래프 탐색은 다양한 곳에서 사용되고 있다.
- 웹 크롤링(구글의 페이지 탐색)
- 소셜 네트워킹(페이스북의 친구 찾기)
- 가비지 컬렉션
- 모델 검사
- 수학적 추측 확인하기
- 퍼즐이나 게임 풀기
여기서는 큐브(루빅 큐브) 맞추기를 이용해 그래프에 대해 자세히 알아본다.
루빅 큐브와 그래프
(2 x 2 x 2) 큐브를 맞추는 과정(사실은 섞는 과정)을 그래프로 생각해보자. 큐브의 특정한 상황을 정점이라고 생각하고, 큐브 조각을 돌리는 과정을 간선이라고 생각하면 모든 과정을 다음과 같은 그래프로 나타낼 수 있다.
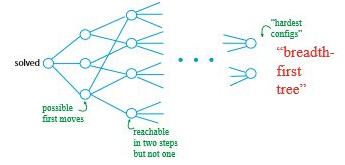
큐브는 한 번 맞추었다고 해서 이전 과정으로 되돌아갈 수 없는 것이 아니다. 따라서 위 그래프는 방향성이 없다.
위 그래프에서 정점은 몇 개일까? 큐브의 한 조각인 큐브릿이 8개 있으므로 $8!$의 상태가 가능하고, 각 큐브릿은 3가지 상태로 회전이 가능하다. 또한, 큐브의 대칭성을 고려하면 $4!$ 로 나눌 수 있고, 큐브릿이 실제 도달할 수 있는 위치까지 고려하면 또 3으로 나눌 수 있다. 최종적으로 정점의 개수는 다음과 같다.
\[\frac{8! \cdot 3^8}{4! \cdot 3}\]
위 그래프에서 주목해야할 다른 요소는 바로 ‘지름’이다. 지름(diameter)은 그래프의 시작점에서 끝까지의 거리를 의미하는데, 큐브를 몇 번 안에 맞출 수 있는지를 알려주기 때문에 신의 숫자로도 불린다. (2 x 2 x 2) 큐브의 경우 지름은 11, (3 x 3 x 3) 큐브는 지름이 20이다. 즉, (3 x 3 x 3) 큐브는 어떤 상태에 있더라도 20번만에 완성시킬 수 있다. 근데 왜 난 못할까 교수님께서 직접 하신 연구에 따르면, (n x n x n) 큐브는 $\Theta(\frac{n^2}{\log{n}})$ 안에 맞출 수 있다고 한다.
루빅 큐브 그래프만 있다면 우리는 큐브가 어떤 상태에 있더라도 완성시킬 수 있다. 큐브가 그래프에서 어떤 정점에 해당하는지를 찾은 다음, 간선을 따라서 하나씩 맞추면 된다. 그래프의 모양을 보면, 중간 부분은 기하급수적으로 커지지만 마지막에는 결국 적은 숫자로 줄어들게 된다.
그래프 표현
그래프 컴퓨터 과학적으로 잘 표현하는 방법은 어떤 것이 있을까? 아마 인접한 정점들을 이용하는 것이 좋을 듯 싶다. 각 정점 $u \in V$ 에 대해, $Adj[u]$ 는 u의 이웃을 저장한다. 방향이 있는 그래프의 경우 나가는 방향에 위치한 정점만 저장한다. 예시를 살펴보자.
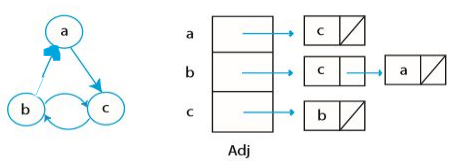
$Adj[b] = {a, c}$, $Adj[a] = {c}$, $Adj[c] = {b}$ 가 되는 식이다. 파이썬에서는 이를 보통 정점을 키(key)로 하는 딕셔너리로 저장하는데, 이렇게 하면 동일한 정점에 대해 여러 가지의 그래프를 생각해볼 수 있다는 장점이 있다.
그래프에서의 너비 우선 탐색 알고리즘 분석
그래프에서 너비 우선 탐색의 의사코드를 살펴보고 탐색의 방법과 필요한 시간에 대해 알아보자.
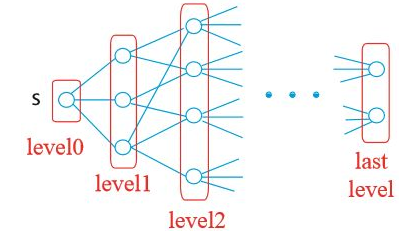
일단 위 그래프에서 몇 가지를 정리해보자. 단계 i는 최소 i개의 간선으로 도달할 수 있는 정점을 의미한다. 단계 0은 시작점에 해당하는 s이다.
다음은 그래프에서 너비 우선 탐색을 구현한 의사코드이다.
BFS(V, Adj, s):
level = {s: 0} # 1
parent = {s: None} # 2
i = 1 # 3
frontier = [s] # 4
while frontier:
next = []
for u in frontier: # 5
for v in Adj[u]: # 6
if v not in level: # 7
level[v] = i # 8
parent[v] = u # 9
next.append(v) # 10
frontier = next # 11
i += 1 # 12
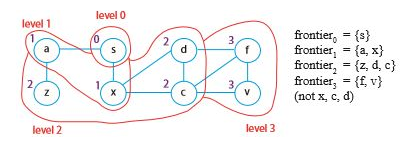
가장 먼저 단계를 저장할 level 딕셔너리를 만들고 s의 단계를 저장했다(# 1). 다음으로 특정 정점 이전 단계의 점들을 저장할 parent 딕셔너리를 만들고, s는 이전 단계가 없으므로 None으로 설정하였다(# 2). 0단계는 이미 끝났으므로 i를 1로 설정하고(# 3), 이전 단계의 정점들에 대해 반복문을 돌리기 위해 frontier라는 리스트를 만들었다(# 4). 이를테면 frontier에 가장 먼저 들어가는 정점은 s, 그 다음은 ${a, x}$, 다음은 ${z, d, c}$ 가 되는 식이다 (위 그림 참고).
이제 반복문에 들어간다. frontier에 대해 반복문을 돌리고(# 5), 각 u에 대해 Adj를 구한다(# 6). u의 Adj에 있는(인접한) v가 이미 탐색한 단계들에 없다면(# 7), level에 v의 단계를 저장하고(# 8) v의 부모로 u를 저장한다(# 9). 그리고 다음에 탐색할 정점으로 v를 추가한다(# 10). 한 frontier에 대한 탐색이 끝났다면 다음에 탐색하기로 정해두었던 next를 frontier로 설정한 뒤(# 11), 단계를 한 단계 늘려서 진행한다(# 12).
위 탐색에 걸리는 시간은 정점에 인접한 점들, 즉 $Adj[v]$ 의 개수에 따라 달라질 것이다. 인접한 모든 점들을 다 탐색해야 그래프 탐색이 끝나기 때문이다.
\[\displaystyle time = \sum_{v \in V}{\vert Adj[v] \vert} = \begin{Bmatrix}\vert E \vert for \, directed \, graphs\\\vert 2E \vert for \, undirected \, graphs\\ \end{Bmatrix}\]그래프의 방향성에 따라 걸리는 시간이 다르다. 쌍방향을 모두 탐색해야하는 방향성 없는 그래프가 2배의 시간이 걸린다.
또한 정점을 탐색하는 시간도 고려해야 한다. 그래서 최종적으로 걸리는 시간은 O(V + E) 시간이 된다. 이는 선형 시간이다.
그럼 최단 경로는 어떻게 구할까? 이미 루빅 큐브를 맞추는 과정에서도 잠깐 언급했지만, 계속 부모(parent) 포인터를 따라가다 보면 큐브를 완성(최단경로에 도달)할 수 있다. parent[v]를 찾고, parent[parent[v]]를 다시 찾고… 이런식으로 하다 보면 최단 경로 조합을 찾을 수 있다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기