개방 주소법의 개념
앞서 우리는 충돌을 방지하는 방법으로 체이닝을 살펴보았다. 이번에는 또 다른 방법으로 개방 주소법을 살펴본다.
개방 주소법(Open addressing)은 연결 리스트와 같은 방법을 사용하지 않고도 모든 항목을 테이블에 저장할 수 있다. ‘원하는 목적에 맞는 슬롯을 찾을 때까지 테이블을 뒤진다’고 생각하면 쉽다. 한 슬롯에는 단 하나의 항목만이 들어간다. 또한, 해시 함수는 삽입, 탐색, 삭제를 위한 키의 슬롯의 ‘탐색 순서’를 정한다. 해시 함수를 표현하면 다음과 같다.
\[h: \, u \times \{0, 1, \dots , m - 1 \} \rightarrow \{0, 1, \dots , m - 1 \}\]처음 u는 키의 집합이다. 그 다음에 등장하는 ${0, 1, \dots , m - 1 }$ 에 주목할 필요가 있는데, ‘해싱을 시도한 횟수’이다. 화살표 오른쪽은 테이블의 슬롯이다.
<$h(k, 0), h(k, 1), \dots , h(k, m-1)$> 은 0부터 m-1 까지의 순열이다. 반드시 순열이어야만 테이블을 낭비하지 않고 마지막 남은 슬롯까지 꽉 채워서 쓸 수 있다. i를 하나씩 늘려가면서 h(k, i)를 다 돌면 테이블에 있는 모든 슬롯을 다 돌게 된다.
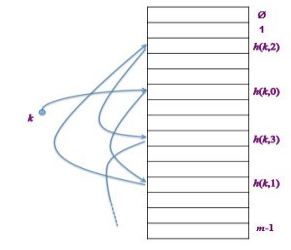
개방 주소법에서의 삽입, 탐색, 삭제
먼저 삽입(insert)에 대해 알아보자. 아주 간단하다. 빈 슬롯을 찾을 때까지 계속 조사하고, 빈 슬롯을 찾으면 항목을 그 슬롯에 넣는다.
for i in xrange(m):
if T[h(k, i)] is None: # 빈 슬롯 발견
T[h(k, i)] = (k, v) # 항목 저장
return
raise full
아래 테이블에 496을 삽입한다고 해보자.
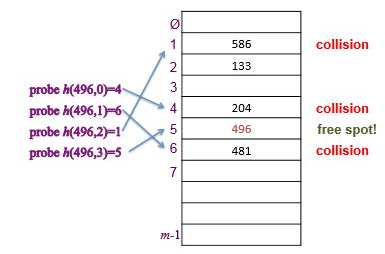
먼저 h(496, 0)을 하게 된다. 이 결과로 4여서 4번째 슬롯으로 갔더니, 이미 204가 들어가 있다. 다음으로 h(496, 1)을 하고(시도 횟수 1 증가!) 결과가 6이어서 6번째로 갔더니 481이 이미 있다. h(496, 2)=1이어서 첫 번째 슬롯으로 가면 586이 있다. h(496, 3)에서야 비로소 비어있는 슬롯(None)을 발견해서 테이블에 추가할 수 있었다.
cf. 496이 4번의 시도에야 슬롯을 할당받은 것을 우연이라고 생각하면 곤란하다. 앞서 해싱 함수의 결과를 ‘순열’이라고 했다. 정해진 순서가 있다는 뜻이다. 즉, 4번째 들어가는 항목이라 3번의 충돌이 발생한 것이다. 다음 항목을 집어 넣는다면 똑같은 순서로 4번의 충돌 후에, 5번째에서야 빈 공간을 찾게 될 것이다.
탐색(search)도 간단하다. 키 k를 찾고 싶을 때, 삽입처럼 키 k를 찾을 때까지 i를 늘려가면서 계속 조사를 하면 된다. 원하는 키를 찾거나(성공) 빈 슬롯을 찾을 때(실패)까지 반복하게 된다.
for i in xrange(m):
if T[h(k, i)] in None: # 빈 슬롯 여부 확인
return None # 종료
elif T[h(k, i)][0] == k: # 키 일치 여부 확인
return T[h(k, i)] # item 반환
return None
삭제(delete)는 생각할 거리가 하나 있다. 단순하게 생각한다면 삭제를 한 후에 해당 슬롯을 다른 빈 슬롯처럼 None으로 표시하면 될 것 같다. 그러나 이러면 다음에 탐색을 할 때 문제가 생길 수 있다. 만약 주어진 순서대로 탐색을 진행하다가 빈 슬롯을 발견하게 된다면? 탐색을 정지된다. 그런데 그 다음 순서에 우리가 찾고자 하는 항목이 있을 수도 있다.
이해가 잘 안될 수 있으니 예시를 보자.

앞서 살펴본 예시이다. 여기서 먼저 delete(586)을 실행해서 586을 지우고 슬롯 1을 빈 슬롯(None)으로 만들었다. 그 다음 search(496)을 실행했다. 슬롯 4, 슬롯 6 순서대로 가다가 슬롯 1에서 반복문이 정지된다. 빈 슬롯을 마주쳤기 때문이다. 우리가 찾고자 하는 496이 버젓이 슬롯 5에 있음에도 None을 마주쳤기에 더 이상 탐색을 진행할 수 없다.
여기서 우리는 그냥 빈 슬롯과 삭제를 통해 비게 된 슬롯을 다르게 취급해야 한다는 사실을 깨달았다. 해결 방법은 매우 간단한데, 삭제를 통해 슬롯이 비게되면 해당 슬롯을 None이 아니라 DeleteMe와 같이 다르게 표시하는 것이다. 삽입에서는 None과 DeleteMe를 같은 의미(빈 슬롯)로 생각하되, 탐색에서는 None을 만나면 정지, DeleteMe를 만나면 계속 진행으로 처리하면 위 문제가 해결된다.
개방 주소법 해시 함수 - 선형 조사
개방주소법에서는 크게 두 가지 해시 함수를 사용할 수 있다. 선형 조사와 이중 해싱이다. 먼저 선형 조사부터 살펴보자.
$h(k, i) = (h^{\prime}(k) + i)$ mod $m$ 처럼 나머지를 사용하는 방식이 대표적인 선형 조사이다($h^{\prime}(k)$ 는 평범한 해시 함수).
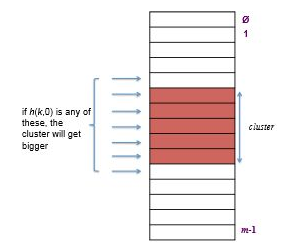
문제점이라면 군집화가 있다. 선형적으로 해시 값을 주므로 테이블이 차는 순서 또한 선형적이다. 즉, 테이블의 특정 부분에 군집처럼 연속적으로 값이 찬 부분이 생기고, 군집의 크기게 $\Theta(\log{n})$ 이 된다. 더 이상 삽입과 탐색이 상수 시간에 이루어지지 않는 것이다.
개방 주소법 해시 함수 - 이중 해싱
선형 조사의 문제점을 이중 해싱으로 해결할 수 있다. 말 그대로 해싱을 2번 한다는 것이다.
$h(k, i) = (h_1(k) + i \cdot h_2(k))$ mod $m$ 처럼 해시 함수를 2개 사용한다. 모든 k에 대해 $h_2(k)$ 와 m이 서로소라면 모든 슬롯을 확인할 수 있다. 가장 많이 사용되는 방법은 $m=2^r$로 하고, $h_2(k)$를 홀수로 정하는 것이다.
이중 해싱을 사용하면 균일 해싱과 비슷한 성능을 낼 수 있다. 균일 해싱이란 각 키가 가지는 조사 순서가 $m!$ 의 무작위 순열 중에 특정 순열일 확률이 균등하다는 뜻이다.
n개의 항목을 m 크기의 테이블에 넣는다고 해보자. 한 방에 삽입에 성공할 확률은 $\frac{m-n}{m} = p$ 이다. 처음에 실패하고 두 번째에 성공할 확률은? $\frac{m-n}{m-1} \geq \frac{m-n}{m}= p$ 이다. 세 번째에 성공할 확률은 $\frac{m-n}{m-2} \geq \frac{m-n}{m}= p$ 가 된다. 모든 시도가 적어도 p 이상의 성공 확률을 가지고 있으므로, 성공까지 기대 시도 횟수는 $\frac{1}{p}$ 라고 할 수 있다. $p = 1-\frac{n}{m} = \alpha$(적재율)을 만족하므로, 기대 시도 횟수는 $\frac{1}{p} = \frac{1}{1-\alpha}$ 도 된다. 즉, 데이터 탐색과 삭제는 $O(\frac{1}{1-\alpha})$ 의 시간이 걸린다.
개방 주소법은 체이닝에 비해 더 나은 캐시 성능을 가진다. 그러나 체이닝에 비해 적재율(적재율이 70%를 넘으면 저하, 1을 넘으면 안 됨)과 해시 함수에 대한 제한이 크다.
암호학적 해싱
우리가 구글에서 로그인을 한다고 해보자. 구글은 우리가 입력한 비밀번호가 어떻게 그 아이디에 맞는 것이라고 판단할까?
가장 단순한멍청한 방식을 생각해보자. 아이디와 비밀번호를 매칭해 놓은 딕셔너리를 만들고, 탐색을 통해 아이디에 맞는 비밀번호를 찾아서 우리가 입력한 것과 대조해보는 것이다. 해커에게는 천국과 다름 없는 방식이다!
해시 함수를 사용하면 조금 더 해커를 당황시킬 수 있다. 암호학에서 사용되는 해시 함수는 다음과 같은 특성을 가지기 때문이다.
- 일방성(One-Way, OW): y가 주어졌을 때, h(x) = y를 만족시키는 x를 찾는 것은 불가능하다. 즉, 무작위 벡터에 대해 그 벡터를 해시 값으로 가지는 입력 값을 찾을 수 없다.
- 충돌 저항(Collision-Resistance, CR): h(x) = h(y)을 만족시키는 두 개의 다른 x는 존재하지 않는다.
- 목표 충돌 저항(Target Collision-Resistance, TCR): x가 주어진 상태에서, x와 x’은 다르고 h(x) = h(x’)인 x’을 찾는 것은 거의 불가능하다.
응용해보자. 우리가 회원가입을 통해 아이디와 비밀번호를 제공하면, 운영자는 비밀번호를 해시로 바꾸어서 아이디와 함께 저장한다. 다음에 우리가 로그인으로 비밀번호를 입력하면, 비밀번호는 해시로 바뀌어서 기존에 저장된 해시 값과 대조되는 것이다. 해커는 물론이고 운영자마저 원래 비밀번호를 알아낼 길이 없다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기