강의 개요
- 강의명: Introduction to Algorithms (파이썬을 이용한 알고리즘의 이해 코스)
- 교수: Erik Demaine, Srini Devadas
- 제작: MIT, 네이버 부스트코스
1차원에서의 극댓값

‘$b \geq a$ 이고 $b \geq c$’이면 그 때의 b를 극댓값(peak)이라고 한다. 만약 배열에서 가장 끝의 값이면 어떨까? 그럼 바로 옆의 값에 비해 크거나 같으면 극댓값이다. 즉, 극댓값은 지역적으로 가장 큰 값인 것이다.
우리가 지금부터 풀 문제는 ‘극댓값이 존재할 경우, 그 값을 찾아라’이다.
cf. 우리의 정의에 의하면 극댓값은 항상 존재한다. 따라서 ‘극댓값이 존재할 경우’라는 단서 조항은 제거해도 무방하다. 하지만 극댓값의 정의가 다르게 될 수도 있다는 것은 알아두자.
1차원에서 극댓값 찾기 - 단순 탐색
가장 간단한 알고리즘은 단순히 탐색을 하는 것이다. 배열의 가장 왼쪽부터 시작해서 오른쪽으로 진행한다.
이 경우에는 평균적으로 $\frac{1}{2}$ 개의 원소를 확인하게 된다. 최악의 경우에는 n개의 원소를 모두 확인해야할 것이다. 복잡도는 $\Theta(n)$ 이다.
1차원에서 극댓값 찾기 - 분할 정복
더 효율적으로 탐색할 수는 없을까? 분할 정복을 이용할 수 있다. 분할 정복의 과정은 다음과 같다.
- 배열의 가운데(
a[n/2])에서 시작. - 왼쪽이 더 크면(
a[n/2] < a[n/2 - 1]) 왼쪽 절반에서 (1번 과정으로 돌아가서) 극댓값 찾기. - 오른쪽이 더 크면(
a[n/2] < a[n/2 + 1]) 오른쪽 절반에서 (1번 과정으로 돌아가서) 극댓값 찾기. - 2, 3번에 아니면 가운데(
a[n/2])가 극댓값.
이 경우 복잡도는 어떻게 될까? ($T(n)$ 은 n 크기의 입력이 주어졌을 때 알고리즘이 하는 일의 양이다.)
\[T(n) = T(n/2) + \Theta(1) = \Theta(1) + ... + \Theta(1) \, (\log_2{n} 번) = \Theta(\log_2{n})\]$\Theta(1)$ 은 a[n/2]을 주변과 비교하기 때문에 생기는 항이다.
이 과정은 앞서 본 단순탐색보다 훨씬 빠르다. n이 1000000인 경우, 파이썬에서 $\Theta(n)$ 의 알고리즘 실행에는 13초가 걸리지만, $\Theta(\log_2{n})$ 알고리즘 실행에는 0.001초만이 걸린다.
2차원에서 극댓값 찾기 - 탐욕 상승 알고리즘
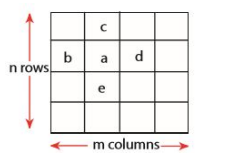
$a \geq b$, $a \geq d$, $a \geq c$, $a \geq e$ 일 때, a를 2차원 극댓값이라고 정의한다.
탐욕 상승 알고리즘으로 극댓값을 찾는 과정은 다음과 같다.
- 임의의 위치에서 시작한다.
- 값이 커지는 방향으로 이동한다.
- 더 이상 이동할 방향이 없으면 그 값이 극댓값이다.
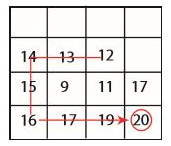
탐욕 상승 알고리즘은 $\Theta(nm)$ 의 복잡도를 가진다.
2차원에서 극댓값 찾기 - 분할 정복
1차원에서 사용한 분할 정복을 2차원에도 적용시켜보자.
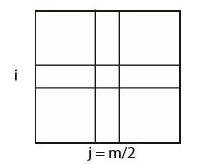
- 중앙 열($j = m/2$)을 선택한다.
- (i, j)에서 극댓값을 찾는다.
- (i, j)를 시작점으로 해서 i행에서 1차원 극댓값을 찾는다.
그런데 위 과정에는 치명적 결함이 있다. 만약, 2차원 극댓값이 i행에 존재하지 않는다면 어떨까?
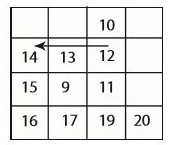
극댓값이 아닌 14를 찾게 된다.
이를 해결한 과정은 다음과 같다.
- 중앙 열($j = m/2$)을 선택한다.
- (i, j)에서 j열의 최댓값을 찾는다.
- (i, j-1), (i, j), (i, j+1)을 비교한다.
- (i, j-1) > (i, j) 이면 왼쪽의 열들을, (i, j-1) < (i, j) 이면 오른쪽 열들을 선택한다. (만약 두 경우 모두 아니라면 (i, j)가 극댓값이다.)
- 선택한 열들에 대해 1로 돌아가 반복한다.

n개의 행, m개의 열이 있는 문제에 대해 복잡도는 다음과 같다.
\[T(n, \, m) = T(n, \, m/2) + \Theta(n) = \Theta(n) + ... + \Theta(n) \, (\log{m} 번) = \Theta(n\log{m})\]
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기